For the past <indeterminate time>, I've been trying to work on an EDA-related tool (formal announcement coming any moment now...) whilst trying to recover from severe, debilitating burnout. This has involved playing around with Rust on "real computers" (i.e. not on microcontrollers) and learning how to write parallel algorithms. This is Part 1 of my learning progress.

Given that I've (in theory) studied all sorts of academic material about algorithms, concurrency, computer architecture, etc. etc., this should be easy, right? Riiiiiiiight...?

Let's find out!

Code for all of this is here

All benchmarks were run on an Apple M1 Max.

A new tool?

Yosys is currently the standard open-source EDA framework. It works quite well for the synthesis and formal verification use cases. However, I wanted a place to freely experiment with... other algorithms (wink).

Yosys RTLIL data structures are also not currently multithreaded, but I predict that multithreading will be critical for handling the... large netlists that my tool would be working with.

With its advertised "fearless concurrency," a natural choice of programming language for this project is Rust.

Minimum viable netlist

For the particular type of neurodivergence that seems to exist in our brain, it is super critical to get something that "looks like it is doing something" as fast as possible. How do we do that?

The structure that I ended up choosing was:

• Cells contain:
  • a type
  • a fixed-size array of (nullable) references to wires (which is actually implemented as a non-fixed-size Vec)
• Wires contain:
  • a list of cells driving the wire
  • a list of cells being driven by the wire
  • a list of cells with bidirectional connections to the wire
• Module inputs/outputs are ignored and handwaved away

This contains the following major differences from Yosys RTLIL:

1. Yosys cells point to wires, but it is hard to go from wires back to the cells connected to them
2. Yosys wires are actually wire bundles of a certain width (which can be 1). This netlist's wires are always a single wire.
3. Similarly, Yosys netlist cell connections can also have a width > 1, and the SigSpec/SigChunk/SigBit types represent details of how this connection is performed.
4. Yosys wires have a name built in to them. When two names are assigned to "the same" wire, two separate Wire objects exist. A vector of SigSigs links them together.
5. Yosys stores a lot more metadata.

Points 2/3/5 differ solely to hack together something simple and minimal as fast as possible. However, points 1 and 4 were intentionally chosen to be different.

For point 1, I am predicting that the types of algorithms I will be interested in will require a lot more arbitrary graph traversals than the typical algorithms in Yosys. Having references in both directions will make this much easier. The trade-off is increased cost (in terms of complexity and performance) keeping the references consistent.

For point 4, I am intentionally treating human-readable names as more akin to metadata than an integral part of wires. This feels like the correct choice for the final application.

Of course, as the rest of the code hasn't actually been written, I don't yet know if these design choices will end up being the right choice.

Make it parallel

The easiest solution that we understood to "just make the thing parallel" is to slap Arc<Mutex<T>> or Arc<RwLock<T>> everywhere:

However, this has an obvious problem in that this data structure inherently contains a lot of cycles. This means that memory will be leaked and never freed. As a further hack, I decided to make all internal references Weak, with the only strong Arc references stored in a global Vec:

With this data structure, no memory will be freed until the entire netlist itself is dropped. Nodes will be free to reference each other with cycles, and upgrading Weak references can't ever fail. However, a lot of extraneous reference counting probably happens.

In order to test out this data structure, we need some algorithms to run on some netlists. For testing, I created a randomly-connected netlist of LUT4s:

The test mutation algorithm inserts a buffer on the output of every LUT4, starting from a certain set of "seed" LUT4s:

Although this is not necessarily completely representative of real designs nor algorithms, it is simple and should at least be useful for getting "order of magnitude" performance numbers.

To make all of this work, we finally need a work-stealing thread pool. The work_queue crate seems like it does what we want. After throwing all of this together, does it work?

A cursory manual inspection of small inputs/outputs seems to indicate that the algorithm is correct (after fixing some bugs). Larger netlists also don't hit any unwrap failures, which is also a good sign. Fearless concurrency! However, performance is a different story:

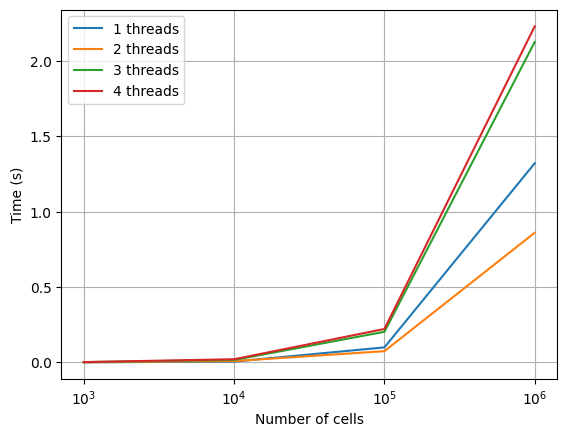
Performance doesn't scale beyond two cores. Hmm.

Looking at what other people did

While throwing together quick hacks, I did also study examples of existing implementations. The first reference I looked at (which I had first read quite some time ago) was a paper titled "Unlocking Fine-Grain Parallelism for AIG Rewriting". This paper references a particular abstraction called "the Galois system" for building parallel graph algorithms.

The papers have been the most useful for me to understand the Galois abstraction have been this and this.

My key takeaways from these papers are:

• "Unordered algorithms with cautious operator implementations can be executed speculatively without buffering updates or making backup copies of modified data"
  • The code I've written is already a "cautious" operator (after minimal modifications)
• "Ordered" algorithms are going to be tricky later, and I will probably need some of them in my program (e.g. clustering)
  • I will have to implement some form of "commit pool" for these

Fixing the worst of the quick hack

The giant mess of Weaks constantly being upgraded/downgraded from Arcs (even though nothing can actually be deallocated) feels like a potential source of performance problems. It really should be replaced by something like an arena/slab allocator. The sharded_slab crate seems like it does what we need.

I also changed the code so that it aborts and retries later (rather than blocking) if an iteration ("operator" in the Galois abstraction) fails to lock all of the nodes it needs.

Final part 1 performance

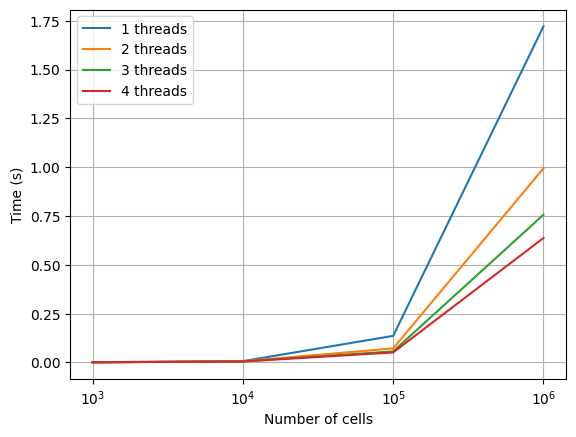
This has fixed the worst of the scaling bottleneck.

Final remarks

Manually acquiring locks and messing with the netlist is very error-prone and cumbersome. I need to figure out a better way to build APIs for this.